30 60 90 triangle sides calculator If you just know the length of one "leg" of a 45 45 90 triangle (figure 8), multiply it by the square root of 2 (about 1414) to obtain the hypotenuse length Clicking "RESET" clears all of the boxes Triangles are classified as "special right triangles"Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleIt will even tell you if more than 1 triangle can be created

30 60 90 Triangle Theorem Ratio Formula Video
30 60 90 triangle side lengths calculator
30 60 90 triangle side lengths calculator-Triangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trig functions30° 60° Triangle Calculator Long Side Short Side Hypotenuse Area Cotangent Formulas of triangle with angle 30̊, 60̊ and 90̊ • area = 05 * long side * short side;




30 60 90 Triangle Calculator Formula Rules
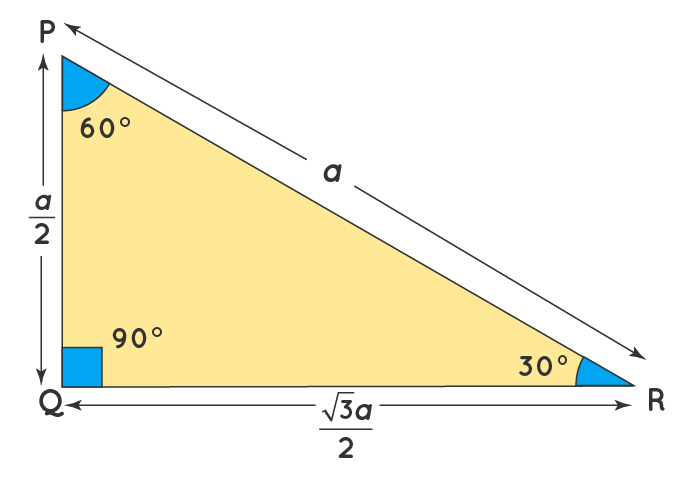
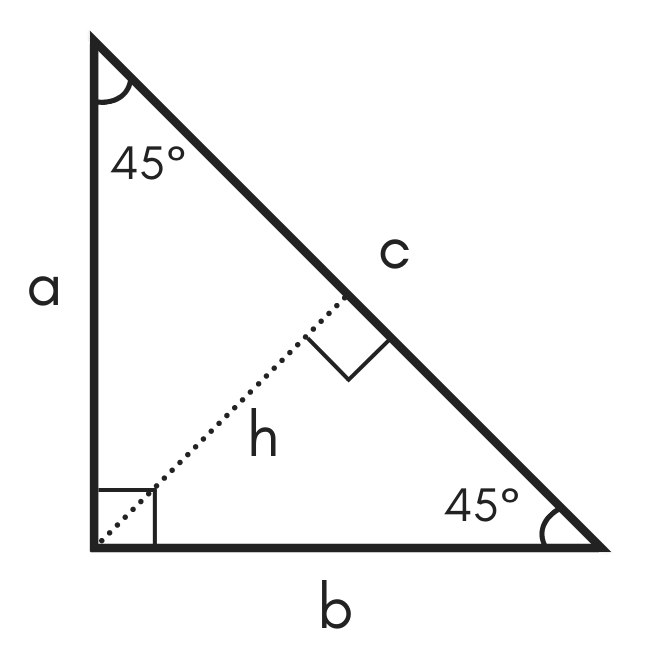
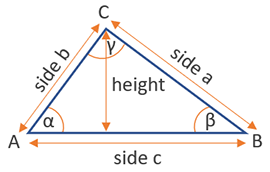
A right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√ (3/2) This means that the hypotenuse is twice as long as the shorter leg and the longer leg is the square root of30 60 90 Triangles A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio o
The right triangle is a special case triangle, with angles measuring 30, 60, and 90 degrees This free geometry lesson introduces the subject and provides examples for calculating the lengths of sides of a triangle👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio oSpecial Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangle
The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of the SATDetermine which set(s) of sides form right triangles 19 15 18 27 Side Lengths 10, 24, 26 In triangle A ABC, ifc is the longest side of the triangle, then Pvthaqorean Triples There are certain sets of numbers that have a very special property in connection to the Pythagorean TheoremA triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Right Triangles Free Math Help
This calculator calculates for the length of one side of a right triangle given the length of the other two sides A right triangle has two sides perpendicular to each other Sides "a" and "b" are the perpendicular sides and side "c" is the hypothenuse Enter the length of any two sides and leave the side to be calculated blank A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another This calculator is designed to give the two unknown factors in a right triangle, assuming two factors are known This calculator is for a right triangle only!




30 60 90 Triangle Explanation Examples



30 60 90 Triangle From Wolfram Mathworld
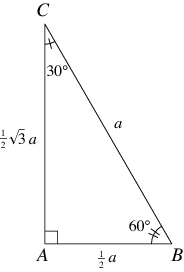
BMI Calculator » Triangle Calculators » Length and Distance ConversionsInch Angle Calculator Isosceles Triangles Measure Angles and Side Lengths by entering 2 known values Enter Side Lengths and either top Angle or Base length to calculate all other side lengths, angles, triangle height and area Top Angle Base Angles 30° Height 3' Area 1559 ft² Trigonometry angle calculator diagramA triangle is a special triangle since the length of its sides is always in a consistent relationship with one another In the belowgiven triangle ABC, ∠ C = 30°, ∠ A = 60°, and ∠ B = 90° We can understand the relationship between each of the sides



30 60 90 Triangle Rules




How To Work With 30 60 90 Degree Triangles Education Is Around
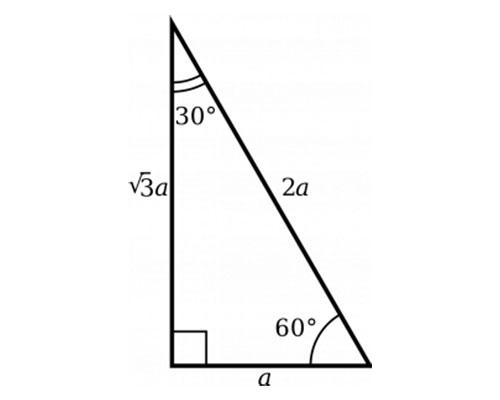
Multiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2Calculator Use A right triangle is a special case of a triangle where 1 angle is equal to 90 degrees In the case of a right triangle a 2 b 2 = c 2 This formula is known as the Pythagorean Theorem In our calculations for a right triangle we only consider 2 known sides to calculate the other 7 unknowns



30 60 90 Triangle Definition Theorem Formula Examples



30 60 90 Triangle Sides Examples Angles Full Lesson
Calc third side of scalene forming lift arm of aircraft dolly/jack (from two known sides and included angle) To improve this 'Scalene triangle Calculator', please fill in questionnaire Age Under years old years old level 30 years old level 40 years old level 50 years old level 60 years old level or over OccupationPractice Using the Triangle to Find Side Lengths with practice problems and explanations Get instant feedback, extra help and stepby The theory applies to the side lengths of a 30 60 90 triangle Tips for Beginners To understand the 3060 ideal triangle, we need to assess a previous topic– the equilateral or equiangular triangular Let's start by attracting a triangle with all three sides the same length This doesn't need to be precise, however the closer the far better



The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 12cm What Is The Length Of The Longer Leg What Is The Length Of The Shorter Leg Quora



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the sideThis calculator exists to compute the area of a triangle, where the three angles of the triangle measure 30, 60, and 90 degrees respectively, and only one other measurement is known It works with a measure of any one side, or by inputting the area or perimeterRight triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator




30 60 90 Triangle Calculator Examples And Formulas




30 60 90 Special Right Triangle Calculator Inch Calculator
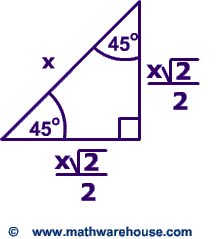
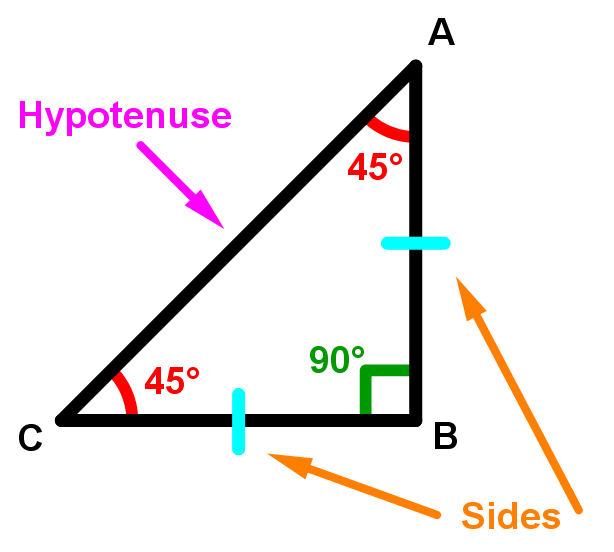
Thanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 inThe 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2 Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides 45 45 90 triangle calculator is a dedicated tool to solve this special right triangle Find out what are the sides, hypotenuse, area and perimeter of your shape and learn about 45 45 90 triangle formula, ratio and rules If you want to know more about another popular right triangles, check out this 30 60 90 triangle tool and the calculator for



45 45 90 Special Right Triangle Calculator Inch Calculator




Triangle Calculator
• perimeter = long side short side hypotenuse;The factors are the lengths of the sides and one of the two angles, other than the right angle All values should be in positive values but decimals are allowed and validSo draw a perpendicular to the base, which also bisects both the third side as well as the 1° vertex angle like this It bisects the 1° into two 60° angles like this Let each of the two halves of the third side be x Now for the right triangle on the left Since this is a 30°60°90° right triangle, we know that the shorter leg (the



30 60 90 And 45 45 90 Triangle Calculator



Triangle Calculator
Calculator Use An equilateral triangle is a special case of a triangle where all 3 sides have equal length and all 3 angles are equal to 60 degrees The altitude shown h is h b or, the altitude of b For equilateral triangles h = ha = hb = hc If you have any 1 known you can find the other 4 unknowns So if you know the length of a side = aTrigonometry Examples Popular Problems Trigonometry Solve the Triangle tri {} {30} {} {60} {} {90} Side Angle b = c = a = A = 30 B = 60 C = 90 Side Angle b = c = a = A = 30 B = 60 C = 90 There is not enough information to solve for all of the sides and angles of this triangle Unknown triangle We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a 2 b 2 = c 2 1 2 (3 –√) 2 = 1 3 = 4 = c 2 4 –√ = 2 = c Using property 3, we know that all triangles are similar and their sides



30 60 90 Special Right Triangle Calculator Inch Calculator




Special Right Triangles Review Article Khan Academy
Math Warehouse's popular online triangle calculator Enter any valid combination of sides/angles(3 sides, 2 sides and an angle or 2 angle and a 1 side) , and our calculator will do the rest!The graphics posted above show the 3 cases of a 30 60 90 triangle If you know just 1 side of the triangle, the other 2 sides can be easily calculated For example, if you only know the short side (figure5), the medium side is found by multiplying this by the square root of 3 (about 1732) and the hypotenuse is calculated by multiplying the short side by 2Right Triangle Calculator To use the right angle calculator simply enter the lengths of any two sides of a right triangle into the top boxes The calculator will then determine the length of the remaining side, the area and perimeter of the triangle, and all the angles of the triangle



Biomath Trigonometric Functions




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
Right Triangle Calculator Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles , the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesA triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the sameThe property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Theorem Ratio Formula Video
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another 30 60 90 triangle sides calculator If you just know the length of one "leg" of a 45 45 90 triangle (figure 8), multiply it by the square root of 2 (about 1414) to obtain the hypotenuse length Clicking "RESET" clears all of the boxes Triangles are classified as "special right triangles" Calculate the cyclist's average speed in mphFind the length of the side x Solution 1 Since the triangle is equilateral, it is also equiangular, and therefore the the angle at B is 60° The height of a triangle is the straight line drawn from the vertex at right angles to the base Therefore, triangle ADB is a triangle



2




A Quick Guide To The 30 60 90 Degree Triangle Dummies
A triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sides




30 60 90 Triangle Theorem Ratio Formula Video




Activity 22 Construct A 30 60 90 Triangle Geogebra
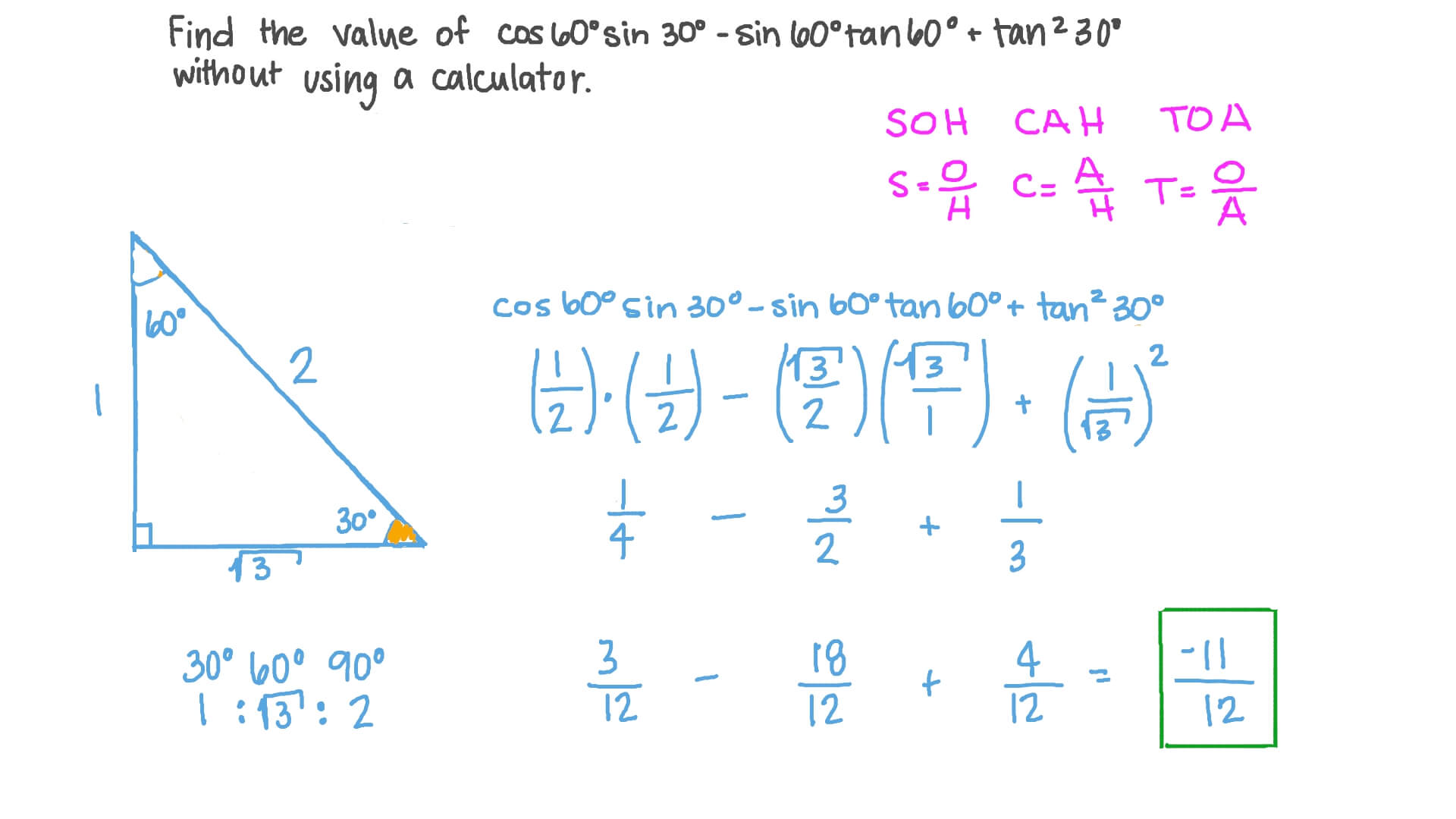



Question Video Using Trigonometric Values Of Special Angles To Evaluate Trigonometric Expressions Nagwa



30 60 90 Triangle Rules Calculator Formula The Free Calculator



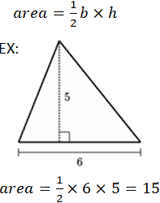
Area Of A Triangle Calculator Calculate Using Sss Sas Asa Ssa Rules
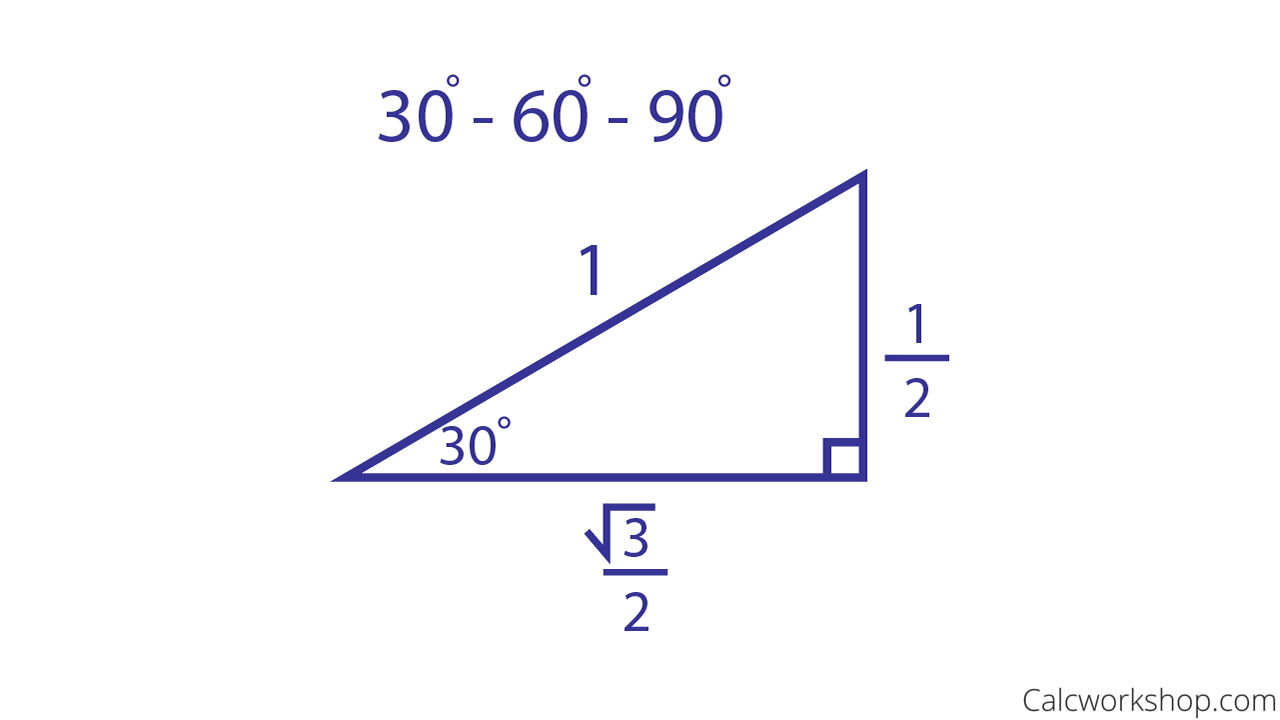



Unit Circle W Everything Charts Worksheets 35 Examples




Theorem Of 45 45 90 Triangle Proof I Chapter 3 Triangles Std




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Triangle Example Problem Video Khan Academy



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle



Triangle Calculator




Velocity



Sin Cos Tan 30 60 90 Triangle




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Calculator Formula Rules




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube



How To Use The Special Right Triangle 45 45 90 Studypug




A Quick Guide To The 30 60 90 Degree Triangle Dummies
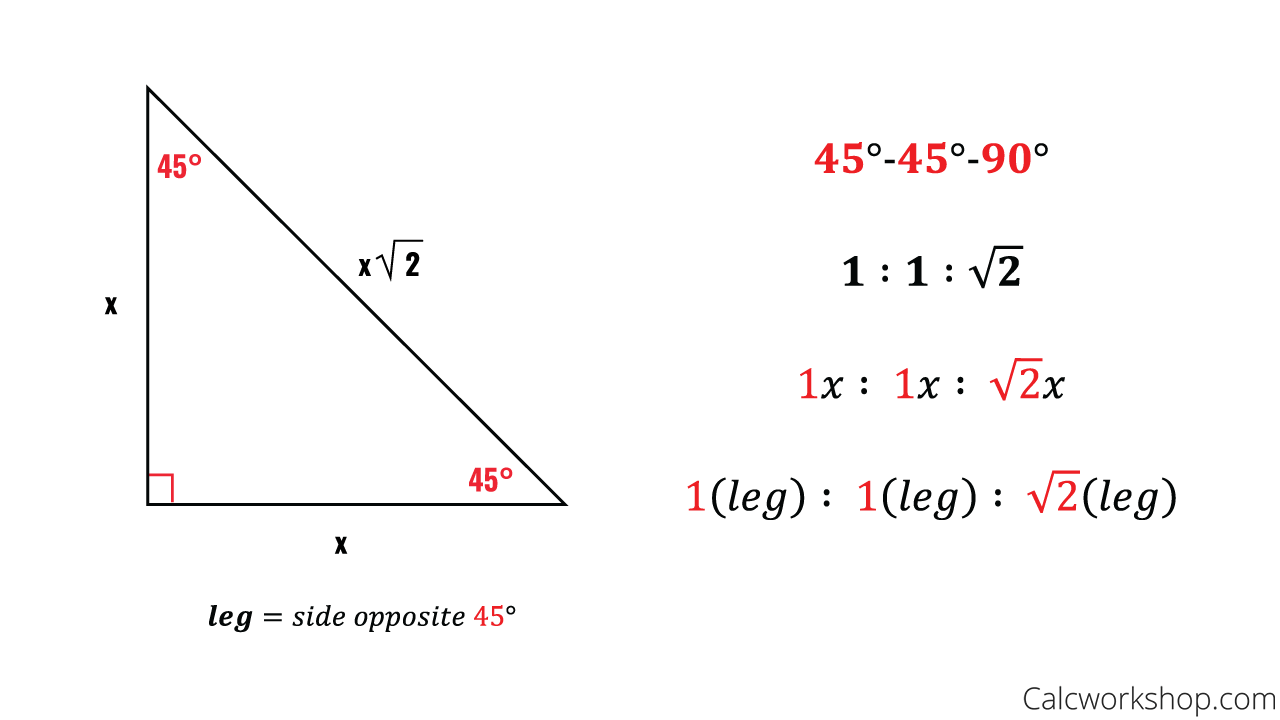



Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Calculator Formula Rules
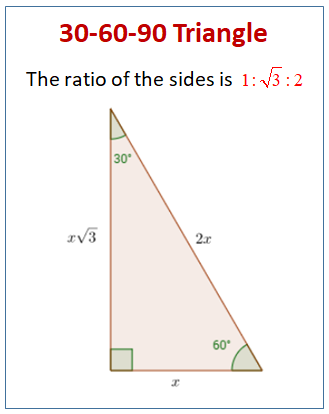



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions
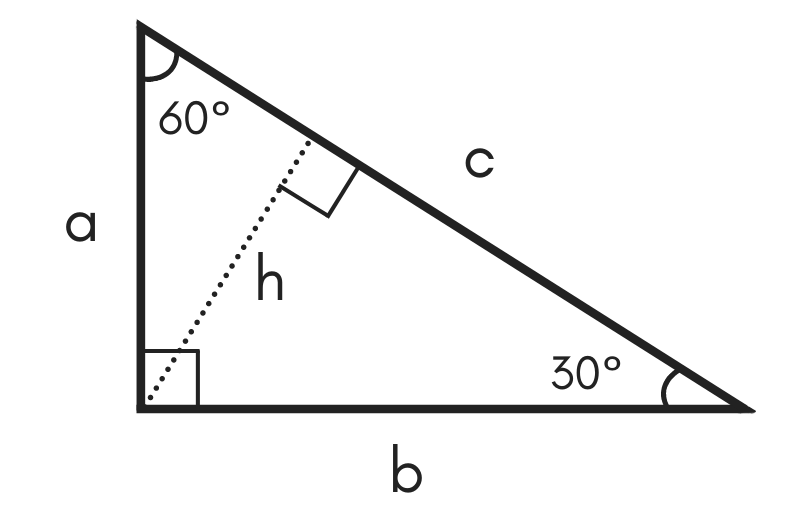



30 60 90 Special Right Triangle Calculator Inch Calculator




The 30 60 90 Triangle Topics In Trigonometry
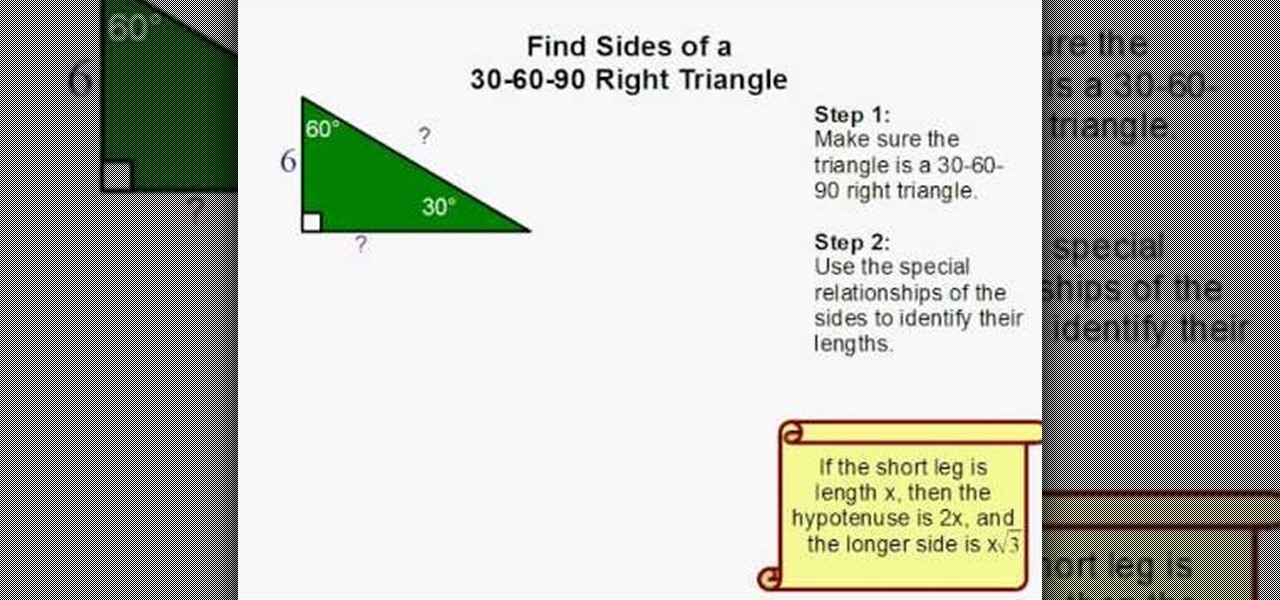



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto



13 3 2 The 30 60 90 Triangle Graphing Calculator By Mathlab User Manual
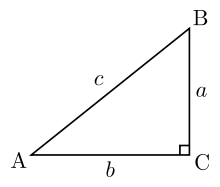



30 60 90 Right Triangle Calculator



1




The Complete Guide To The 30 60 90 Triangle




30 60 90 Special Right Triangle Calculator General Knowledge Book Right Triangle Electrical Engineering Books
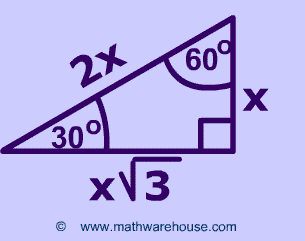



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



1
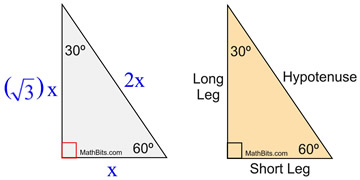



Special Right Triangles 30 60 90 Mathbitsnotebook Ccss Math




Velocity
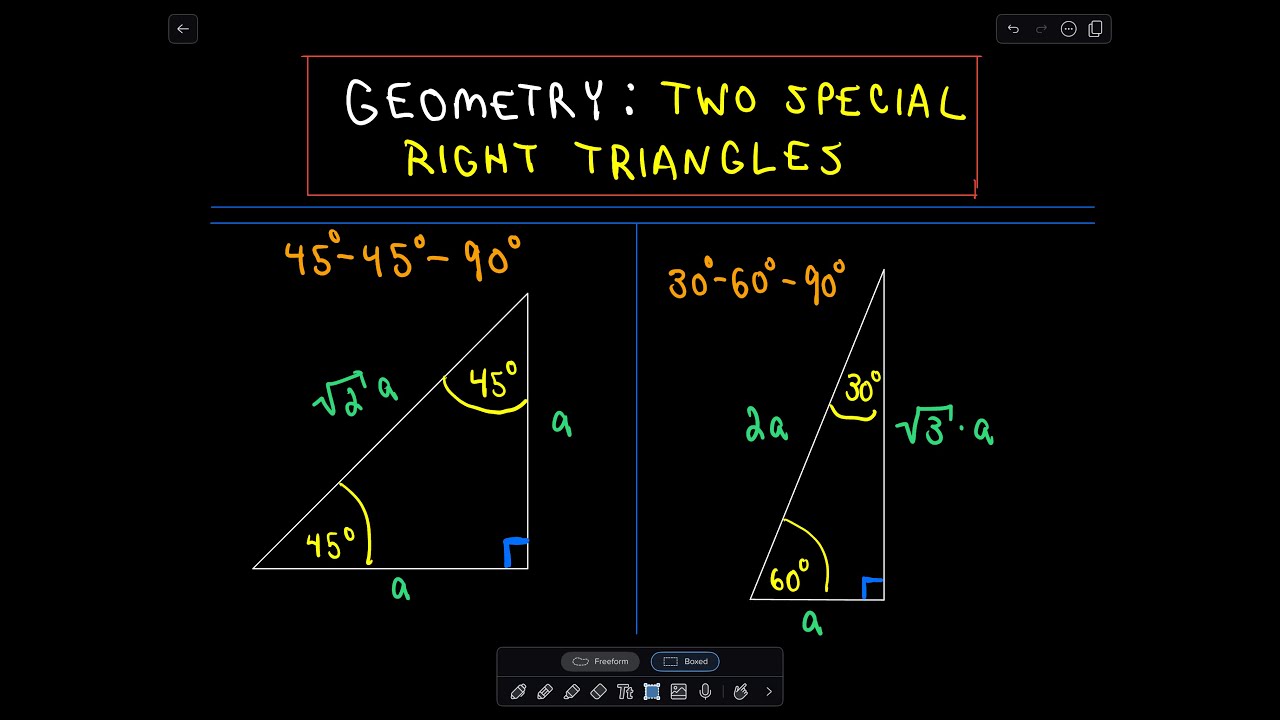



Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




The Complete Guide To The 30 60 90 Triangle




Solved 4 Special Triangles And The Unit Circle No Chegg Com
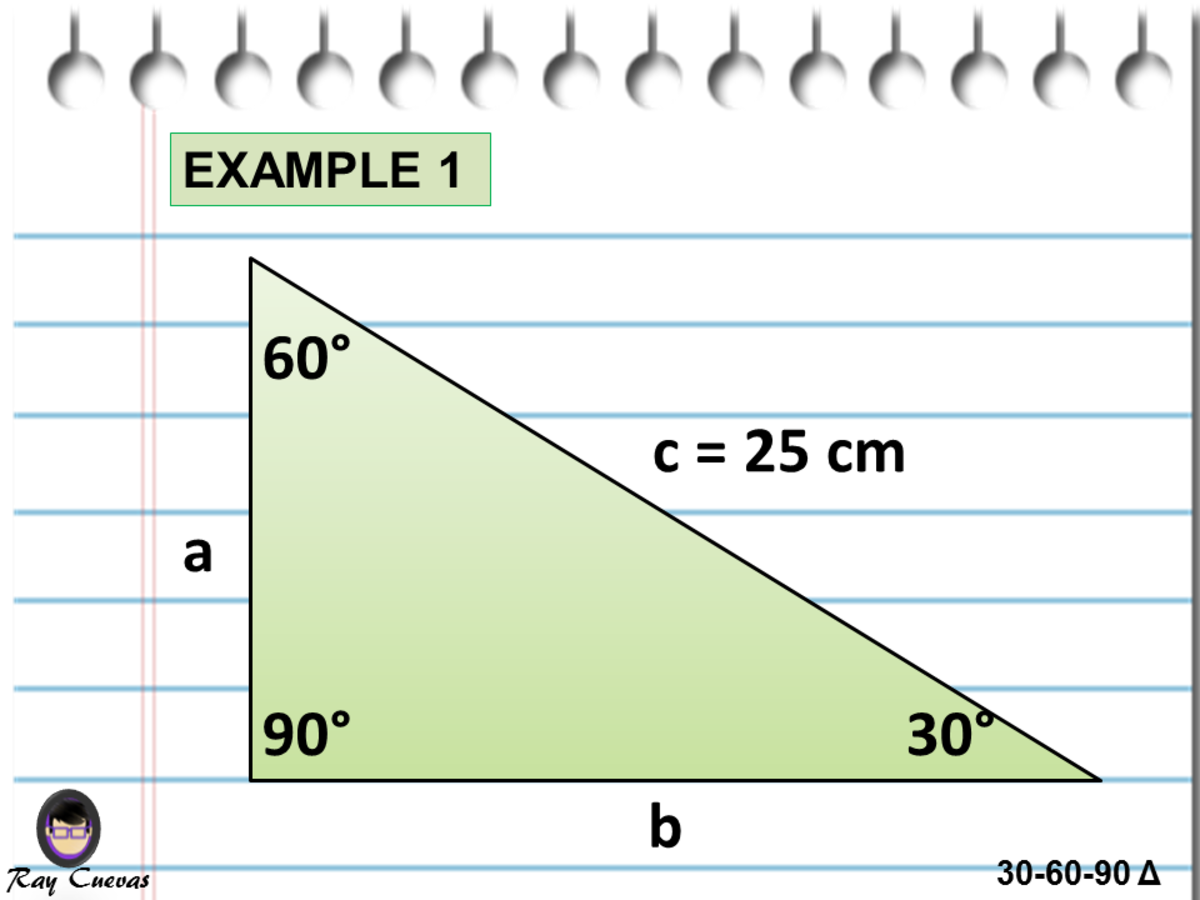



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet
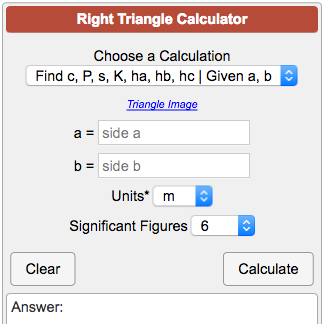



Right Triangles Calculator



30 60 90 And 45 45 90 Triangle Calculator




30 60 90 Triangle Rules Calculator Formula The Free Calculator



1




30 60 90 Right Triangle Side Ratios Expii




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



30 60 90 And 45 45 90 Triangle Calculator




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



30 60 90 And 45 45 90 Triangle Calculator




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies
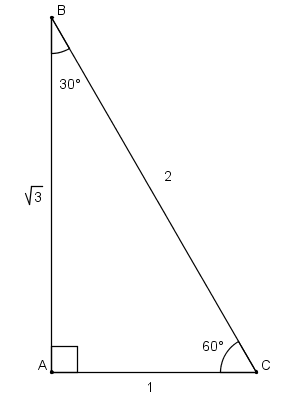



Find The Value Of The Sine Or Cosine Functions Of An Angle Given A Point On Its Terminal Side Precalculus




How To Calculate The Missing Side Length Of A Triangle Youtube
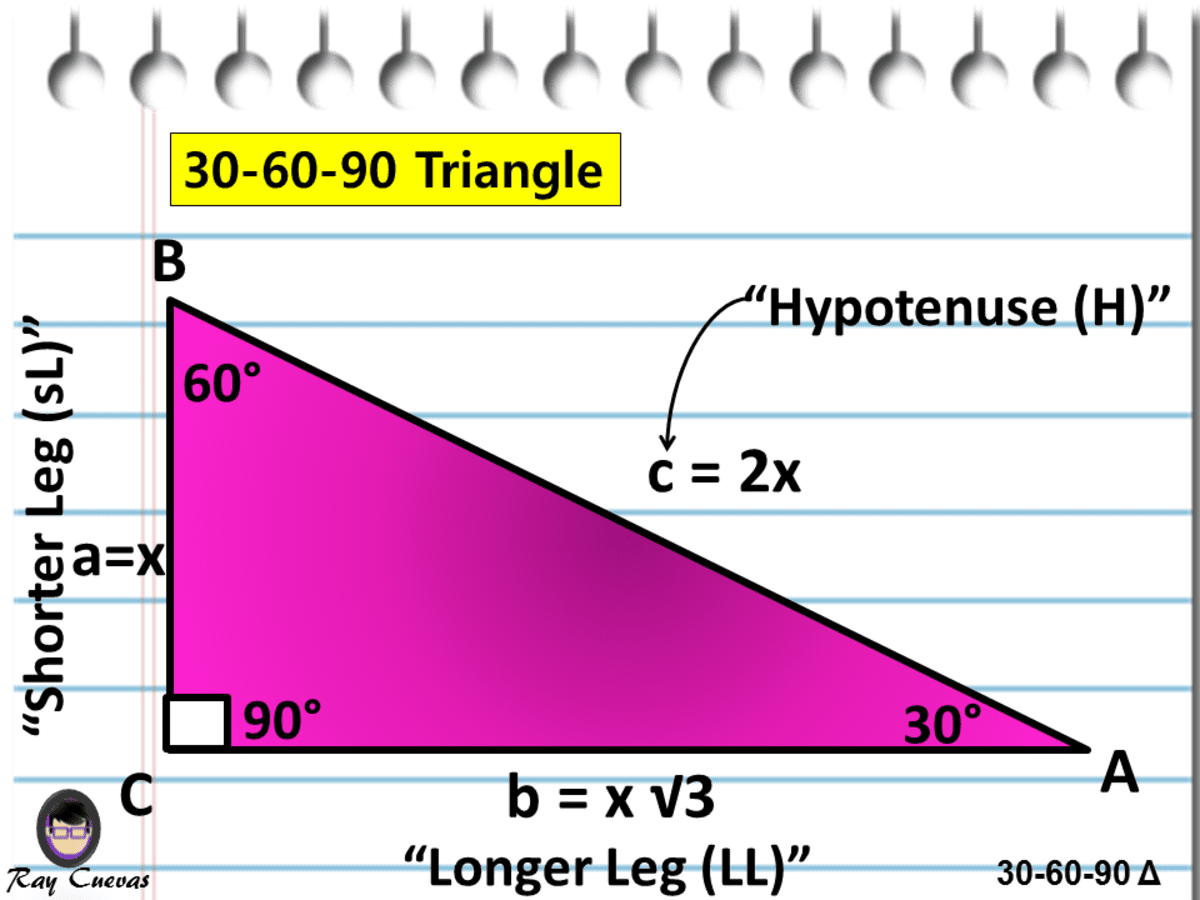



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Triangle Calculator Square Footage Area
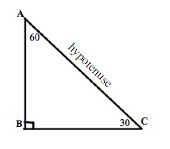



Special Triangles Isosceles And 30 60 90 Calculator




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Formulas Rules And Sides Science Trends




Right Angle Triangle Trigonometry Review Ck 12 Foundation
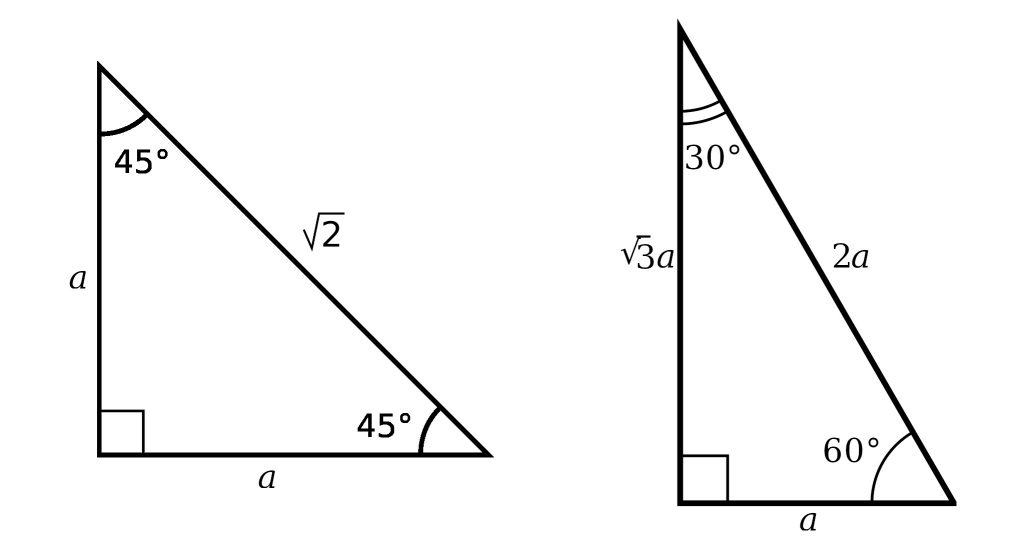



Special Right Triangles Sss a Examples Included



30 60 90 Triangle From Wolfram Mathworld



Triangle 30 60 Calculator Endmemo




30 60 90 Triangles



Special Triangles Isosceles And 30 60 90 Calculator
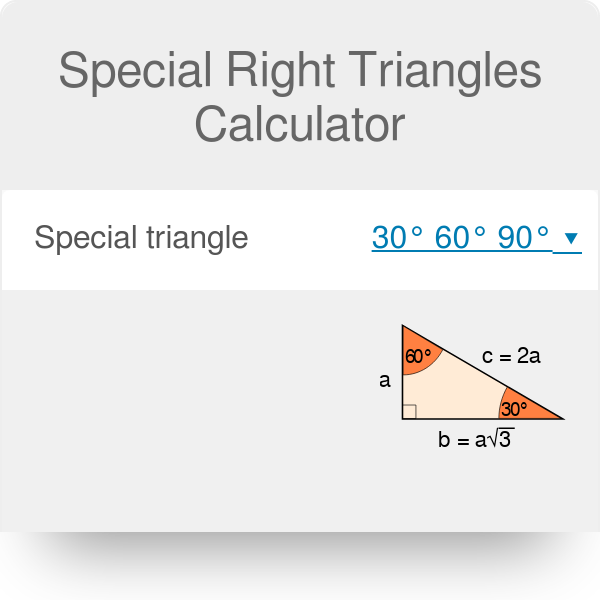



Special Right Triangles Calculator Formula Rules



Triangle Calculator
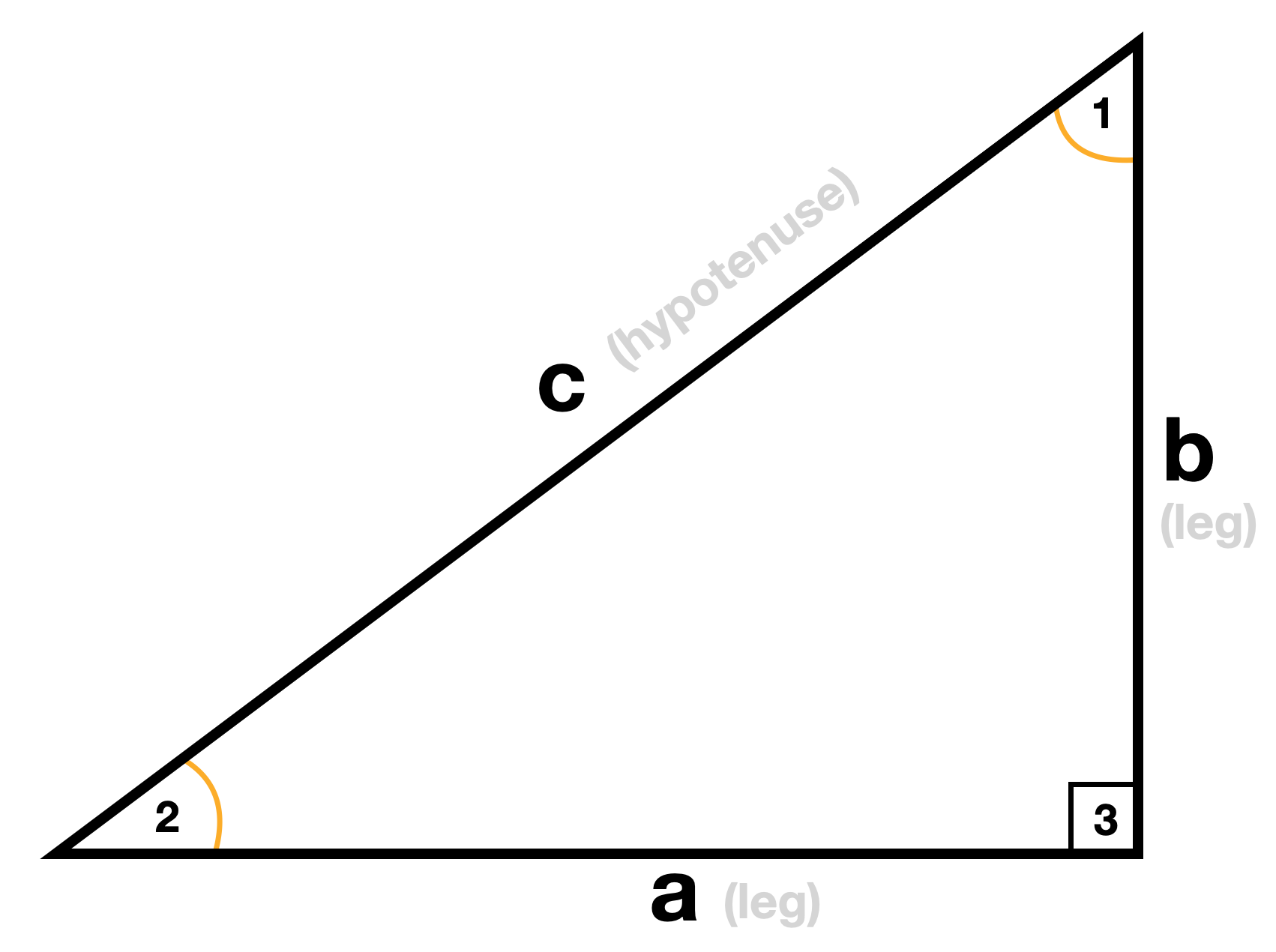



Right Triangle Calculator Pi Day
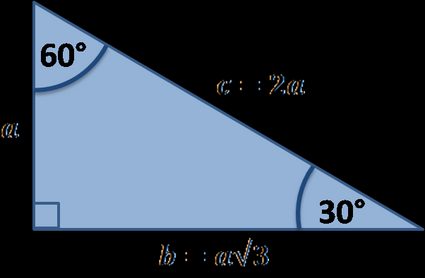



30 60 90 Triangle Calculator Formula Rules



13 3 2 The 30 60 90 Triangle Graphing Calculator By Mathlab User Manual



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Theorem Ratio Formula Video
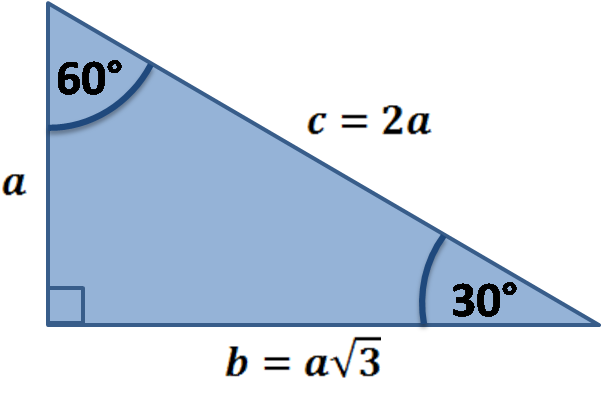



30 60 90 Triangle Calculator Online Discount Shop For Electronics Apparel Toys Books Games Computers Shoes Jewelry Watches Baby Products Sports Outdoors Office Products Bed Bath Furniture Tools Hardware




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



What Are Some Differences And Similarities Between 30 60 90 Triangles And 45 45 90 Triangle Quora
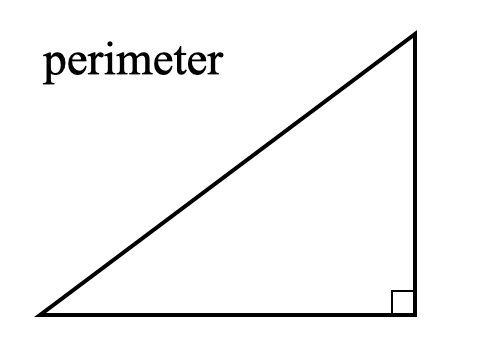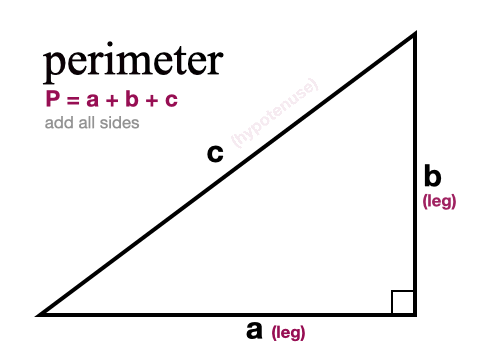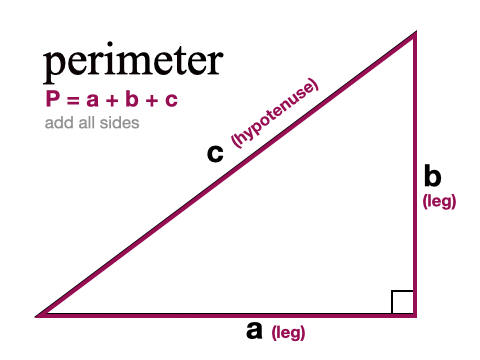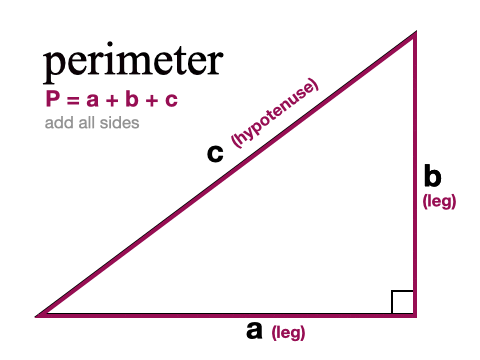



Right Triangle Calculator Pi Day




45 45 90 Triangle Calculator Formula Rules
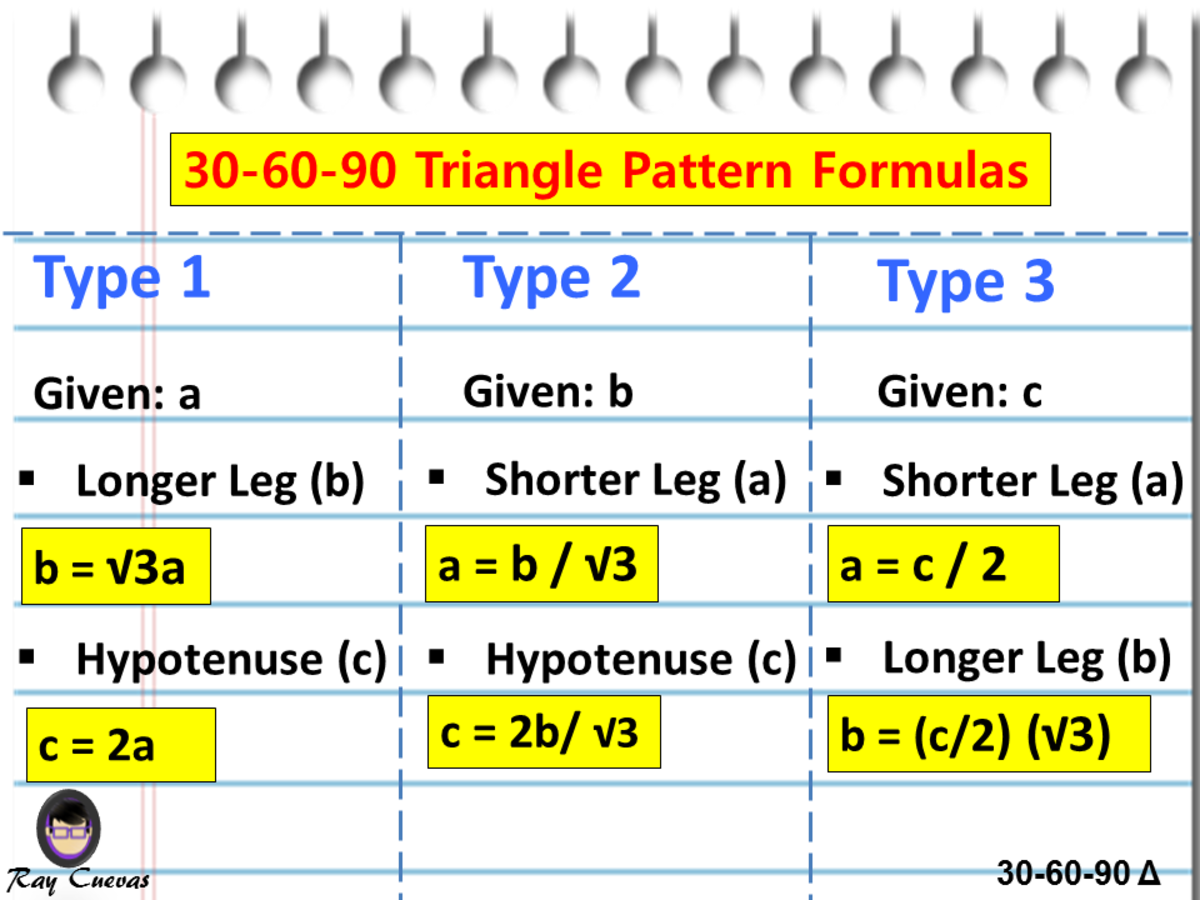



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




View Question Practice Problems 1 In A 30 60 90 Triangle What Is The Length Of The Hypotenuse When The Shorter Leg Is 8m



Special Right Triangles Activity Builder By Desmos



45 45 90 And 30 60 90 Triangles Zona Land Education


